State space models (SSM) promised a way out of attention’s quadratic scaling. Mamba delivered on that promise: linear compute, constant memory, competitive perplexity. But researchers kept noticing the same failure mode. Ask the model to recall something specific from early in a long context, and performance drops. Not always, not catastrophically, but consistently enough that it matters.
The reason comes down to a single architectural choice that makes SSMs efficient in the first place. Three papers at ICLR 2026 independently attacked this same limitation. That convergence tells you something about how fundamental the problem is.
The Compression Tradeoff
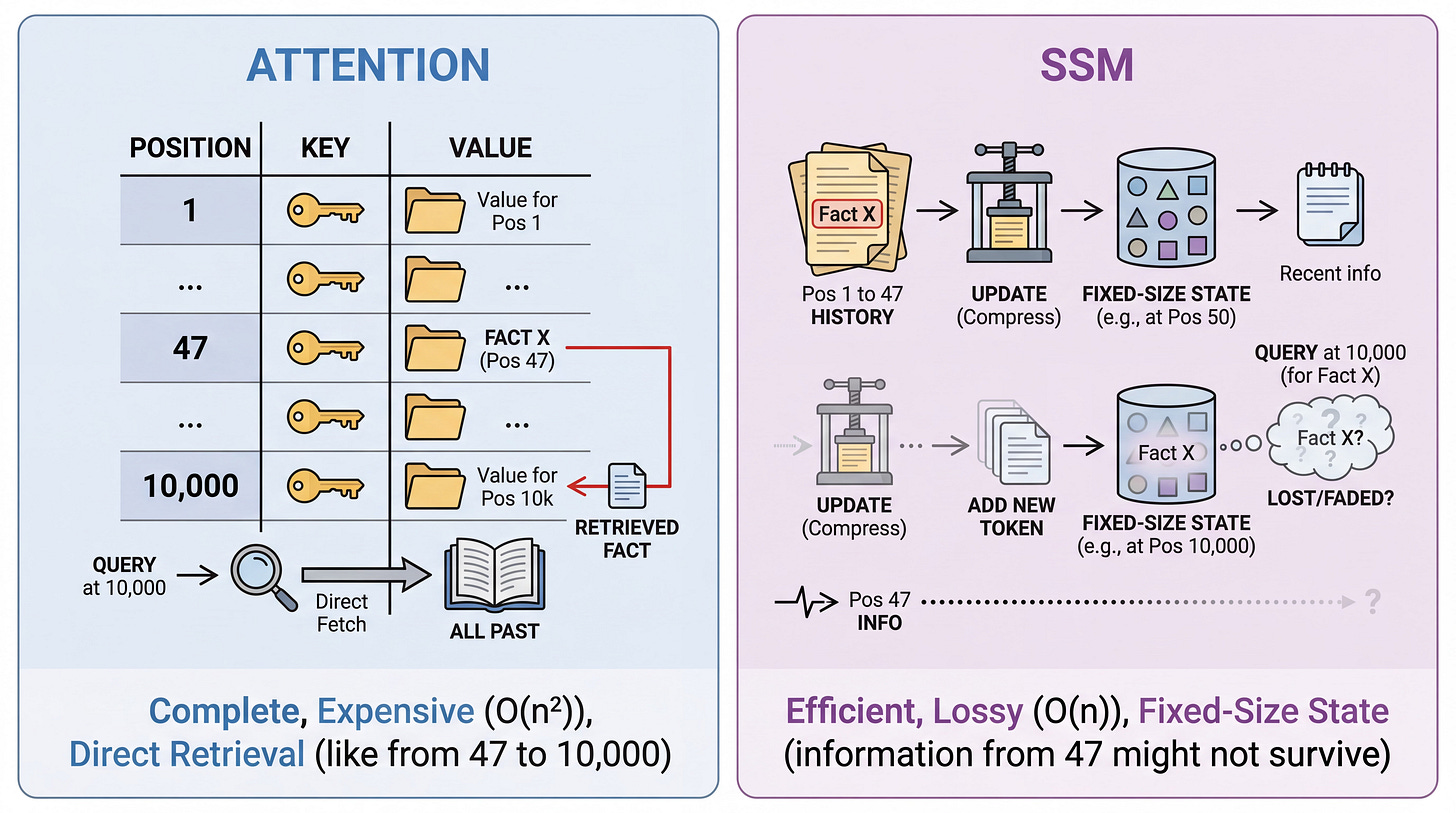
Attention works like a lookup table. The model stores keys and values for every position, then retrieves what it needs. When something from position 47 matters for predicting position 10,000, attention can fetch it directly. This is expensive (quadratic in sequence length) but complete.
SSMs work differently. They compress the entire history into a fixed-dimensional state vector that updates with each new token. The state carries forward information about everything that came before, but it can only hold so much. When the model needs information from position 47 at position 10,000, that information either survived thousands of state updates or got overwritten by more recent content.
This explains a pattern that confused early Mamba adopters. The model matches Transformers on perplexity (predicting likely next tokens draws on statistical regularities that compress well) but struggles on recall-intensive tasks (retrieving specific earlier facts requires that those facts survived in state). The fixed-size state is a lossy compression of history.
That lossy compression is both the source of efficiency and the source of limitation.
Three Ways to Add Memory Back
Each of these ICLR’26 papers answers the same question differently: how do you increase effective memory without giving up the efficiency that makes SSMs attractive?
Multiply the states internally
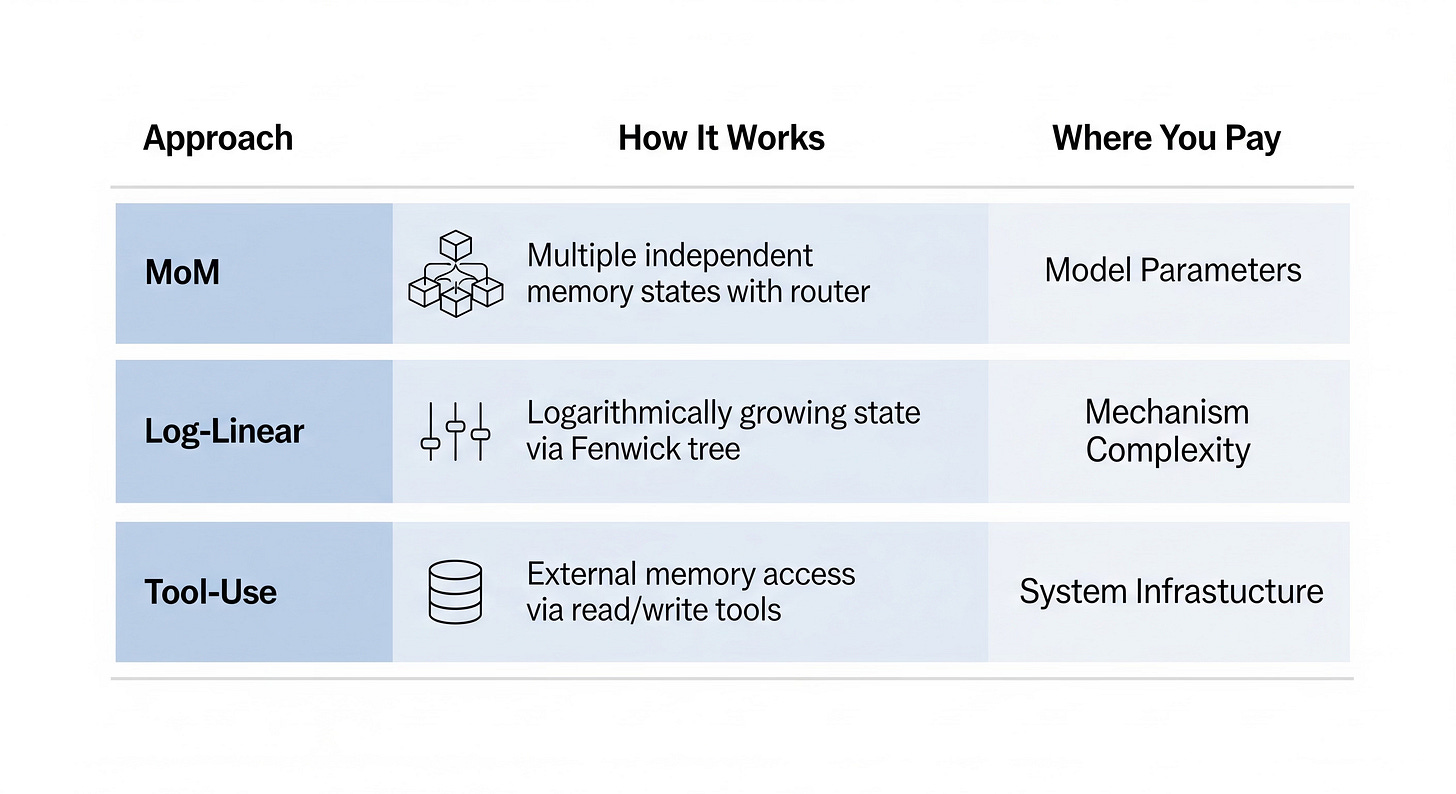
MoM: Linear Sequence Modeling with Mixture-of-Memories takes the direct approach. Instead of forcing everything through one state, use multiple independent memory states. A router network directs input tokens to specific states based on content, so related information clusters together rather than competing for the same limited capacity.
The tradeoff: you’re adding parameters and routing logic. The model gets larger and the forward pass gets more complex. But everything stays self-contained. No external systems, no inference-time dependencies, just a bigger internal memory.
Bridge back toward attention
Log-Linear Attention asks whether the choice between quadratic attention and linear SSMs is really binary. The paper develops an attention variant that sits between these extremes, achieving parallelizable training and fast sequential inference while partially recovering attention’s ability to access specific positions directly.
The tradeoff: you’re buying back some of what SSMs gave up. Complexity lands somewhere between pure SSM and full attention, which means some of the simplicity benefits disappear. But you get a middle ground that might hit a better point on the capability/efficiency curve for your specific use case.
Externalize memory entirely
To Infinity and Beyond: Tool-Use Unlocks Length Generalization in State Space Models starts with a theoretical result: SSMs with fixed-size state provably cannot solve certain long-form generation problems. The information-theoretic constraints are real, not just engineering limitations. But the paper then shows that giving SSMs interactive access to external tools (retrieval systems, explicit memory stores) sidesteps these constraints entirely.
The tradeoff: the model stays simple, but you push complexity into the surrounding system. You now need infrastructure for tool access, retrieval indices, memory management. The SSM becomes one component in a larger architecture rather than a self-contained solution.
The pattern
All three approaches are variants of “add more state.” They differ in where you pay the cost. MoM pays inside the model parameters. Log-Linear pays in the attention mechanism. Tool-use pays outside the model in system complexity. No free lunch, just different checks to different accounts.
Want to Go Deeper
Here are some more papers from ICLR 2026 on Mamba or SSM.
Universal Position Interpolation: Training-free fix for hybrid Mamba-Transformer models that collapse beyond their training context length
A Theoretical Analysis of Mamba’s Training Dynamics: Shows how Mamba learns to filter task-relevant features during training
From Markov to Laplace: Explains Mamba’s in-context learning through Laplacian smoothing
AIRE-Prune: Post-training state pruning using impulse-response energy as the compression metric
HADES: Reinterprets Mamba2 as an adaptive filter bank using graph signal processing
Mamba-3: Next architecture iteration targeting remaining quality gaps with Transformers
Want me to go over any of these directions in a dedicated issue? Let me know in the comments.